One idea being communicable in multiple different ways is a recurring
phenomenon in mathematics. This talk will explore an accessible example.
Namely, we will discuss three ideas (see below), which on the surface, seem
somewhat different. However, we will reveal that all three communicate
the same basic concept, and justify this with accessible examples.
- A partition of a set
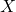 is a collection of subsets
is a collection of subsets 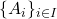 that is pairwise disjoint:
that is pairwise disjoint:
![Rendered by QuickLaTeX.com \[A_i\cap A_j=\emptyset, \text{~when~}i\neq j, \]](https://mathclub.trubox.ca/wp-content/ql-cache/quicklatex.com-d33ddb262412380a77f9b64e37869084_l3.png)
and whose union is
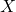 :
:![Rendered by QuickLaTeX.com \[\bigcup_{i\in I} A_i=X. \]](https://mathclub.trubox.ca/wp-content/ql-cache/quicklatex.com-9ecd624c48b7cdfd3fc9abf5253a90ec_l3.png)
- An equivalence relation on a set
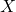 is a relation
is a relation  that is reflexive,
that is reflexive,
symmetric, and transitive. - A surjection
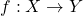 is a function whose range is equal to its
is a function whose range is equal to its
codomain. That is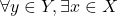 such that
such that 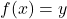 .
.