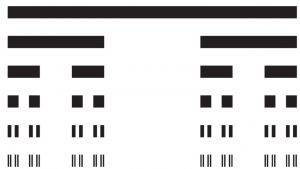
Georg Cantor first came up with the idea of Cantor sets when he discovered a generalization of perfect sets that were nowhere dense; however, this was not the only paradoxical property. To construct the Cantor ternary set, begin with the interval [0,1] and perform iterations where you delete the open middle third interval from each remaining line segment. The Cantor set is known as the limit set of this process. An interesting question is to ask what points belong to the Cantor ternary set. As it turns out, using base three notation can be extremely informative when approaching this problem. Construction of Cantor sets will be discussed, with emphasis on the Cantor ternary set. Properties such as cardinality and self-similarity will also be investigated.